W przypadku miłośników łamigłówek matematycznych wieże Hanoi - klasyczna zagadka znana również jako wieże Hanoi, Wieża Brahmy lub Wieża Lucasa - są intrygującym wyzwaniem zakorzenionym w zasadach matematycznych. Puzzle składa się z trzech prętów i zestawu dysków o różnej wielkości, ułożonych od największego na dole do najmniejszej u góry, tworząc stożkowy kształt.
Celem jest przeniesienie wszystkich dysków z lewicowej pręta do prawej prętu w najmniejszych możliwych ruchach, przy jednoczesnym przestrzeganiu tych podstawowych zasad:
- Tylko jeden dysk można przesuwać jednocześnie.
- Można przesunąć tylko najwyższy dysk na pręcie, umieszczając go na pustym pręcie lub z większym dysku.
- Dysk nie można umieścić na mniejszym dysku.
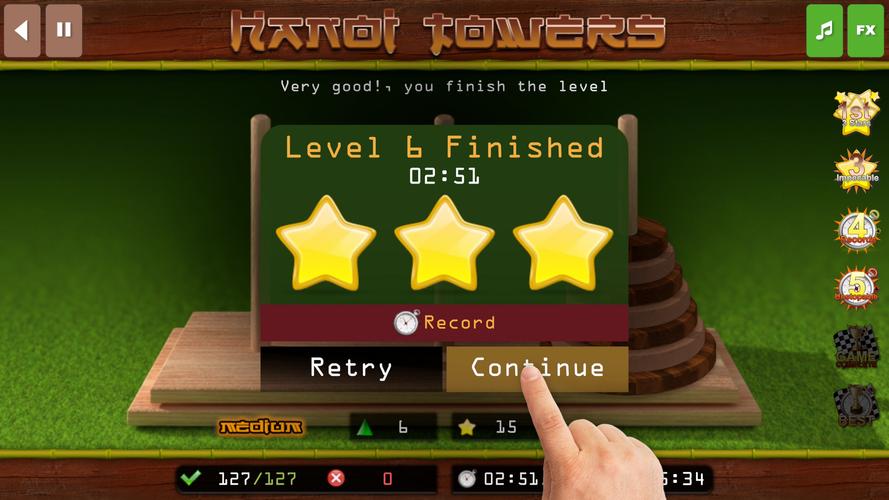
Gra przechodzi przez poziomy, przy czym każdy nowy poziom dodaje dodatkowy dysk do początkowego stosu na lewym pręcie, zwiększając złożoność w miarę postępów. Po ukończeniu poziomu gracze otrzymują informacje zwrotne:
- Osiągnięto numer poziomu.
- Całkowity czas na zakończenie poziomu.
- Czy ustalono rekord czasu.
- Trzygwiazdkowy ranking oparty na:
- Osiągnięcie minimalnych wymaganych ruchów.
- Ukończenie poziomu bez błędów.
- Ustawienie rekordu czasu.
Aby triumfować w grze, gracze muszą z powodzeniem ukończyć wszystkie siedem poziomów. Na zakończenie podsumowanie wyników podkreśla szczegóły, takie jak czasy ukończenia, rekordy, dokładność, rankingi gwiazd i osiągnięte osiągnięcia. Osiągnięcia te obejmują kamienie milowe, takie jak zdobycie pierwszych trzech gwiazdek, osiąganie nienagannych występów kolejno, ustalanie wielu rekordów czasowych, bezbłędnie kończąc grę i osiągając najszybszy czas.
Mamy nadzieję, że ta matematyczna łamigłówka okaże się przyjemną, jak i stymulującą intelektualnie!
Co nowego w wersji 1.49.0
Ostatnia aktualizacja 10 sierpnia 2024 r. To wydanie zawiera kompletne przepisanie z ulepszonym silnikiem, oferując lepszą wydajność i szerszą kompatybilność. Najważniejsze informacje obejmują:
- Wprowadzenie opcji poziomu trudności.
- Ulepszona funkcja dotykowa w gładszej rozgrywce.
- Rozdzielczość wszystkich błędów obecnych we wcześniejszych wersjach.